Las Matemáticas y Kanban
El otro día al ir a enseñarle un video de Youtube a un amigo empezaron a aparecer en el móvil videos sobre matemáticas y estadística. Ante esta avalancha de videos inesperados entre los que tuve que navegar para enseñarle lo que buscaba, surgió la incómoda pregunta “pero Rober, ¿y tú para qué usas esto?”. Ésta se parece bastante a la típica pregunta que alguna vez he oído “¿pero esto de las matemáticas tiene utilidad para mi trabajo?”
Tras esta pregunta, como en todo sistema capitalista, mi amigo había creado una necesidad que hasta entonces no tenía y que debía ser cubierta: la necesidad de explicarme a mí mismo y a los que me conocen como uso las matemáticas en mi trabajo diario. Y este es básicamente el origen de este artículo en el que pretendo contar la utilidad de las matemáticas y la estadística en los equipos con los que colaboro, tanto en el día a día como en las reuniones de revisión del flujo o servicio.
El Método Científico, el Método Kanban y las Matemáticas
Comenzamos con una breve explicación de lo que es cada cosa:
El método científico se fundamenta en una serie de pasos que van desde la observación y el reconocimiento del problema hasta el análisis de los resultados y la comunicación de los hallazgos realizados.
El método Kanban es un enfoque eficaz para que las organizaciones logren una mayor agilidad empresarial basado en seis prácticas generales:
- Visualizar el flujo
- Limitar el trabajo en curso
- Gestionar el flujo
- Hacer explícitas las políticas
- Implementar ciclos de feedback
- Mejorar de manera colaborativa
Las matemáticas, por su parte, estudian las propiedades de los números y las relaciones que se establecen entre ellos.
Aunque las matemáticas se pueden utilizar en la gestión de cualquier tipo de trabajo en el que queramos incorporar la mejora continua, me voy a centrar en Kanban. ¿Por qué? Porque es con los equipos que aplicaban un sistema Kanban, donde he tenido una relación más prolongada que nos ha permitido analizar datos y poder trabajar la mejora continua aplicando el método científico.
Ahora que todos nos encontramos en la misma página, vamos a ver el detalle de como aplicar de forma práctica estos tres conceptos en un sistema kanban.
Aplicación del Método Científico y las Matemáticas en Kanban
Supongamos que empezamos a trabajar con un equipo que quiere mejorar los servicios que ofrece. Un buen paso inicial consiste en aplicar el método STATIK (System Approach to Introduce Kanban).
Este método nos permite tener una visión de los objetivos, las debilidades y las oportunidades de mejora. El resultado obtenido nos ayuda a comenzar con el primer paso del método científico: la observación.
STATIK nos ayuda a conocer el sistema, detectar las insatisfacciones y analizar la capacidad y la demanda, lo que nos permite reconocer los posibles problemas. El modelado del sistema y la implementación de este nos facilita además lanzar hipótesis en busca de mejoras.
Tras la hipótesis y la predicción de mejoras viene el siguiente paso: la experimentación. Es en este punto donde entran de lleno las métricas que se han definido en las fases anteriores. Entre las más utilizadas están el Lead Time, Cycle Time, Delivery rate o Throughput, Tiempo de las peticiones en cada estado, el WIP (Work in Progress) y el cálculo de la eficiencia del flujo.
Finalmente llegamos a la fase de análisis. Es aquí donde comparamos los experimentos propuestos con las métricas obtenidas y aplicamos nuestros conocimientos matemáticos para poder llegar a conclusiones.
Es en este punto donde:
- estudiaremos variables como media, moda, percentiles (50,85,98), revisaremos los histogramas del lead time y cycle time
- generaremos el diagrama de flujo acumulado para detectar posibles cuellos de botella en nuestro flujo
- aplicaremos teorías de la probabilidad como la ley de los grandes números para poder obtener conclusiones
- estudiaremos la desviación típica
- analizaremos las curvas asociadas a las diferentes clases de servicio (estudiando si son distribuciones exponenciales, gaussianas o pareto)
- y en función del tipo veremos que partes del servicio se pueden mejora
En la práctica
Pongo un ejemplo, un poco más concreto, para aclarar a qué me refiero:
Supongamos que estamos trabajando con un equipo en el que algunos de los principales objetivos son disminuir el tiempo, que tardamos en atender a nuestros clientes, y conseguir ser más predecibles. Para conseguir mejorar, nos centramos en estudiar las propiedades matemáticas del lead time de una de nuestras clases de servicio.
Para ello comenzamos con un cálculo sencillo, en este caso la media. Ésta solo nos ofrecerá información “fiable” si nuestro servicio es robusto y lineal. En cualquier otro caso, la variación es tan alta que no nos aporta demasiada información.
Después de la media, continuaremos con los percentiles (50 (mediana), 66, 85, 98). Nos permiten dividir nuestro servicio en 100 partes. Gracias a ellas, podemos explicar a nuestro cliente de una forma sencilla, que un X% de los pedidos de la clase Y tardan en entregarse al cliente menos de Z días.
Seguimos con la moda, que nos indica el valor más repetido dentro de nuestra clase de servicio.
Ahora, para poder continuar necesitamos poder determinar la distribución de probabilidad que sigue el servicio que estamos analizando. Dependiendo de esta distribución, necesitaremos más o menos puntos de medidas para poder ofrecer unas previsiones del servicio con un reducido % de error.
Es decir, utilizaremos los tiempos que hemos ido recogiendo durante un periodo. Pero debe tratarse de un período que nos proporcione datos suficientes para poder obtener conclusiones. Y aquí debemos tener en cuenta que el número de datos necesarios depende de la curva asociada a nuestro servicio.
Y por último, para analizar la distribución, comenzamos representando el histograma del lead time. Una representación que nos ofrecerá información más clara y concreta sobre el servicio que los parámetros anteriormente calculados.
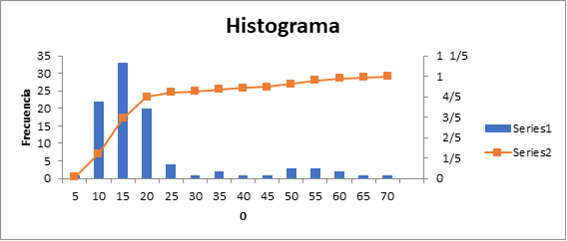
En nuestro caso, aplicamos la ecuación de Weibull, para determinar el tipo de distribución de probabilidad de nuestra muestra.
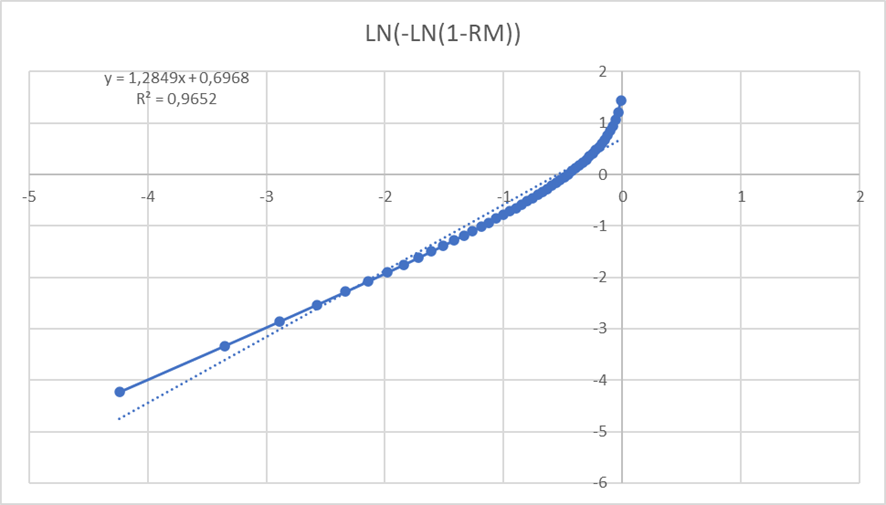
En el ejemplo vemos que, tras realizar el cálculo, obtenemos k =1,28. Este k lo que indica es que es una distribución super-exponencial y para este tipo de distribuciones podemos utilizar la ley de Little como herramienta predictiva.

Además, si dividimos el percentil 98 entre la mediana (percentil 50), podemos ver en base al resultado si nuestra distribución es muy dispersa o está concentrada, lo que nos permite dar más garantías en caso de que esté concentrada.
Este es un breve ejemplo de las aplicaciones de las matemáticas, utilizadas en Kanban. Pronto compartiré el paso a paso matemático que utilizamos para calcular la k en la ecuación de Weibull, qué significan los diferentes resultados, cómo analizamos la dispersión de la muestra, cuándo realizamos determinados cálculos y cómo todos estos datos los incluimos en las reuniones de revisión de flujo o del servicio, para dar herramientas a los equipos en la búsqueda de la mejora continua.
Roberto Cano. 2 de diciembre de 2021